[剑指Offer] Day 24: Mathematics

Authored by Tony Feng

Created on May 5th, 2022

Last Modified on May 30th, 2022

Task 1 - Q14,I. 剪绳子

Question

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。其中，2 <= n <= 58

Solution 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


class Solution: # Dynamic Programming
    def cuttingRope(self, n: int) -> int:
        dp = [0] * (n+1)
        dp[2] = 1   # 2 = 1 + 1; res = 1 * 1 = 1
        for i in range(3, n+1): 
            for j in range(2, i):   # Starting from 2 because 1 doesn't change the result in multiplication
                dp[i] = max(dp[i], j*(i-j), j*dp[i-j])
                # 1) Keep unchanged
                # 2) Cut length of j and keep the rest line unchanged
                # 3) Cut length of j and continue to cut following the way of dp[i-j]
        return dp[n]

Solution 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


class Solution: # Optimized Dynamic Programming
    def cuttingRope(self, n: int) -> int:
        dp = [0, 1, 1]
        for i in range(3, n+1):
            res1 = max(1*dp[(i-1)%3], 1*(i-1))
            res2 = max(2*dp[(i-2)%3], 2*(i-2))
            res3 = max(3*dp[(i-3)%3], 3*(i-3))

            dp[i%3] = max(res1, res2, res3)

        return dp[n%3]

Solution 3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


class Solution: 
    '''
    1) The length of each sub-line should be as equal as possible.
    2) The optimal length of each sub-line is 3.
    '''
    def cuttingRope(self, n: int) -> int:
        if n < 4: 
            return n - 1

        a, b = n // 3, n % 3
        if b == 0: 
            return pow(3, a)
        elif b == 1: # The last length is 1. Instead, we deal with the last two sub-lines, because 2*2 > 3*1
            return pow(3, a - 1) * 4
        else: # b == 2
            return pow(3, a) * 2

Explanation

Solution 1
- Time Complexity: O(N²)
- Space Complexity: O(N)
Solution 2
- Time Complexity: O(N)
- Space Complexity: O(1)
Solution 3
- Time Complexity: O(1)
- Space Complexity: O(1)
- Assuming we have a line with length $n$ , we want to cut it evenly into $m$ pieces with the length of $x$ .
  - The product $x * \frac{n}{x}$ reaching maximum happens when $x * \frac{1}{x}$ is the maximum.
  - Therefore, we need to find the integer $x$ so that $x^{\frac{1}{x}}$ is the largest.
  - Apply log to the equation, $y = x^{\frac{1}{x}} \rightarrow ln(y) = ln(x^{\frac{1}{x}})$
  - Calculate the derivative of $y$ in respect to $x$ : $\frac{\partial y}{\partial x} =\frac{1-\ln x}{x^{2}} x^{\frac{1}{x}} = 0$
  - When $x_0 = e$ , it reaches maximum. Because $x$ is an integer, $x = 3$ is the best solution.

Task 2 - Q57,II. 和为s的连续正数序列

Question

输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class Solution: # Sliding Window
    def findContinuousSequence(self, target: int) -> List[List[int]]:
        i, j = 1, 2
        total, res = i+j, []

        while j - i > 0:
            if total == target:
                res.append(list(range(i, j+1)))
                
            if total >= target: # We need to remove the first num
                total -= i
                i += 1
            else:               # We need to add the next num
                j += 1
                total += j

        return res

Explanation

Time Complexity: O(N)
Space Complexity: O(1)

Task 3 - Q62. 圆圈中最后剩下的数字

Question

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

Solution 1

1
2
3
4
5
6
7
8
9


class Solution: # Recursion
    def lastRemaining(self, n: int, m: int) -> int:
        def recur(remain, cnt):
            if remain == 1:
                return 0
            else:
                return (recur(remain-1, cnt) + cnt) % remain

        return recur(n, m)

Solution 2

1
2
3
4
5
6
7


class Solution: # Iteration
    def lastRemaining(self, n: int, m: int) -> int:
        p = 0
        for i in range(2, n+1):
            p = (p + m) % i

        return p

Explanation

F(curNum, m) = (F(curNum−1, m) + m) % curNum

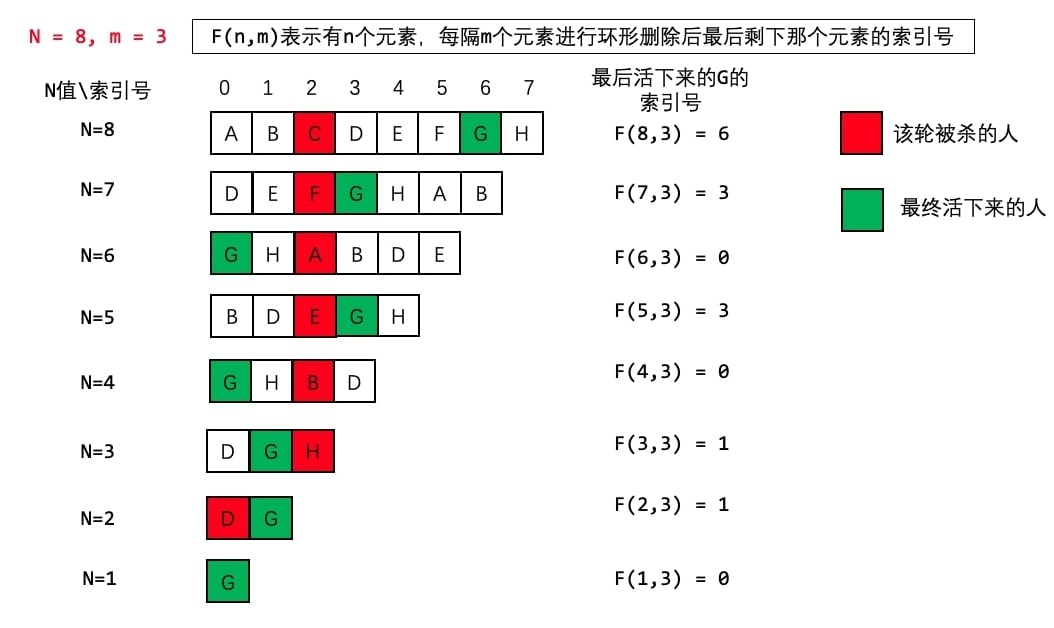
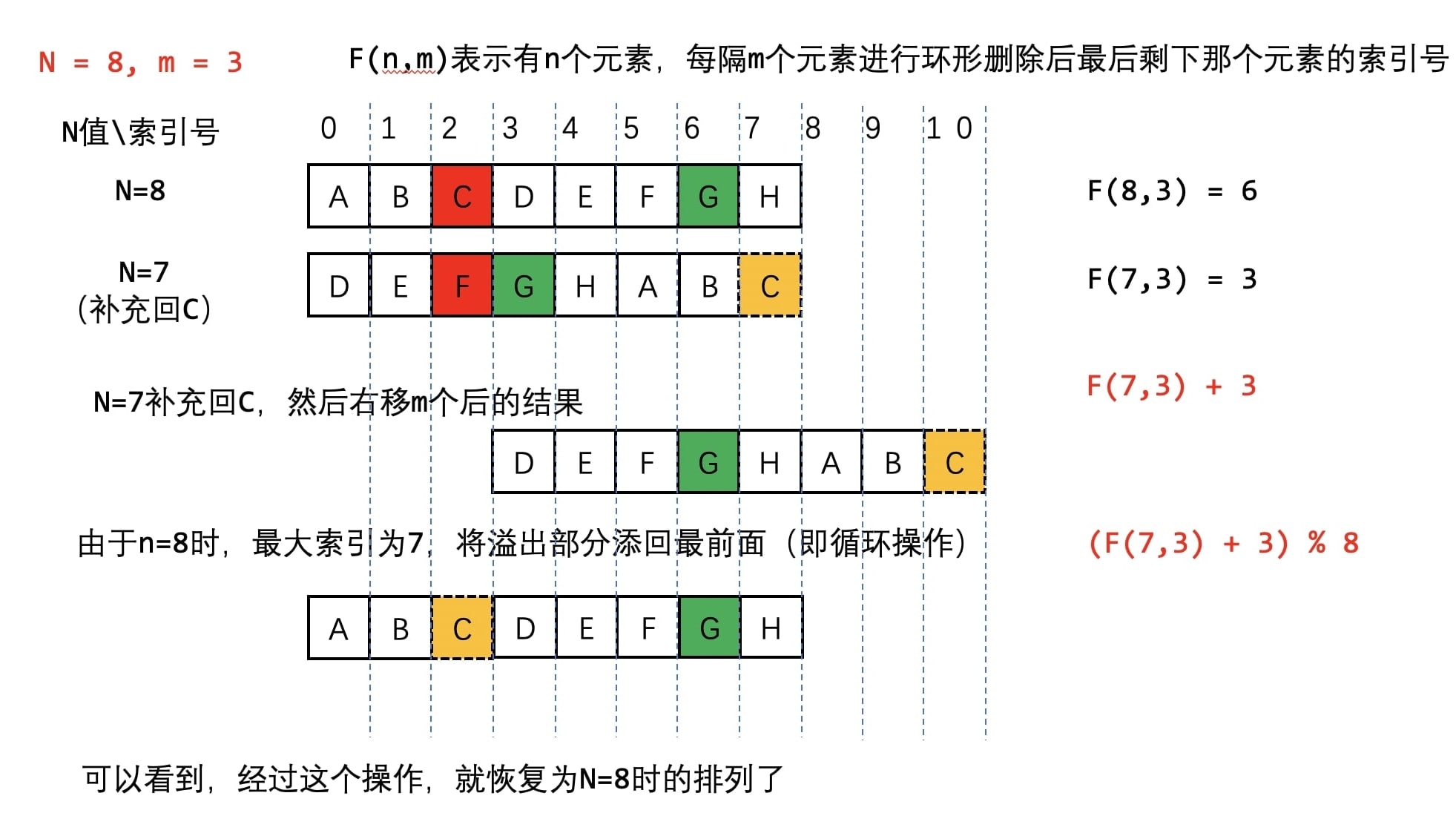
Solution 1
- Time Complexity: O(N)
- Space Complexity: O(N)
Solution 2
- Time Complexity: O(N)
- Space Complexity: O(1)