Authored by Tony Feng

Created on Oct 18th, 2022

Last Modified on Oct 20th, 2022

Intro

This sereis of posts contains a summary of materials and readings from the course CSCI 1460 Computational Linguistics that I’ve taken @ Brown University. The class aims to explore techniques regarding recent advances in NLP with deep learning. I posted these “Notes” (what I’ve learnt) for study and review only.

Multi-layer Perceptron

• MLP doesn’t readily support long, sequential inputs
• MLP doesn’t consider encoding word order, essentially a BOW model.
• Inputs either become muddy (adding everything together, i.e., “bag-of-vectors”) or too large (concatenating everything)
• “bag-of-vectors” classifiers are common and often work well for basic applications

Recurrent Neural Network (RNN)

Architecture

The basic idea is generation of word $i+1$ depends on word $i$ plus “memory” of words generated up to $i$.

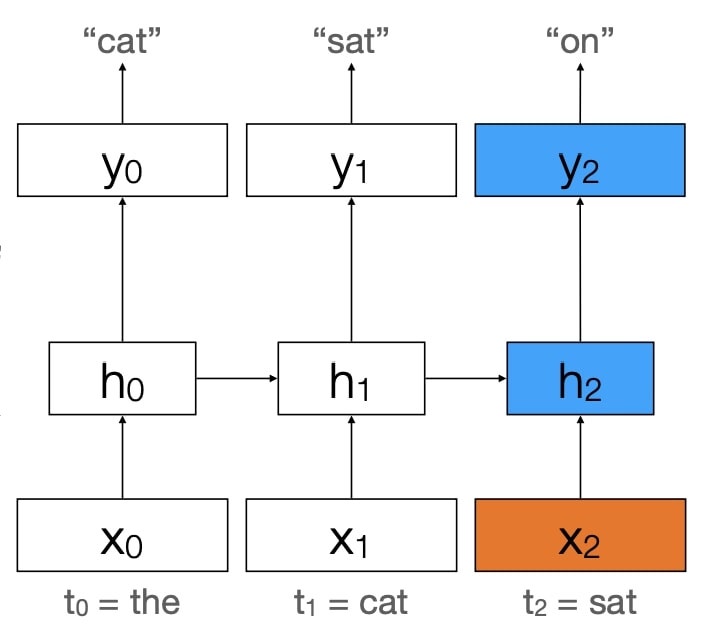
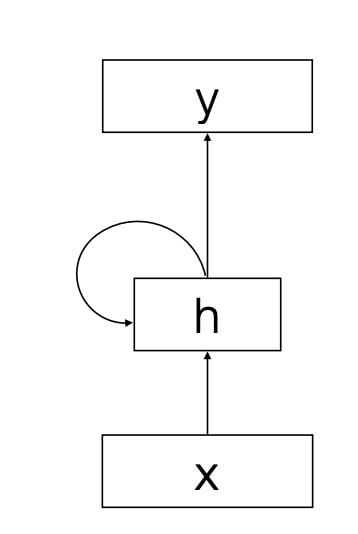
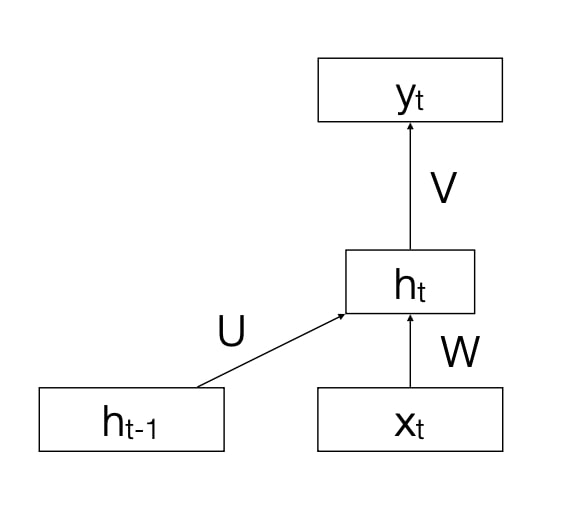
$$h_{t}=g\left(U h_{t-1}+W x_{t}\right)$$ $$y_{t}=f\left(V h_{t}\right)$$

Inference

1
2
3
4
5
6

function ForwardRNN(x, rnn) -> sequence y:
    h_0 <- 0
    for i <- 1 to length(x) do:
        h_i <- g(U * h_(i-1) + W * x_i)
        y_i <- f(V * h_i)
    return y

Training Considerations

• In practice, using unrolled and padded to a fixed length is better for batching.
• When producing word $i$, predict based on the real $i-1$, not the predicted $i-1$ (which is likely wrong).

Long-Short Term Memory (LSTM)

Motivation

• RNNs struggle with long range dependencies.
• Vanishing gradients makes it hard to update early hidden states for long sequences.

Architecture

Overview

• Introducing a “gating” mechanisms to manage the hidden state/ memory
• Passing through “gates”
  • “Forget” gate removes information no longer needed
  • “Add” gate adds new information likely to be useful in the future
  • “Output” gate
• Adding explicit previous “context” in addition to prior hidden state

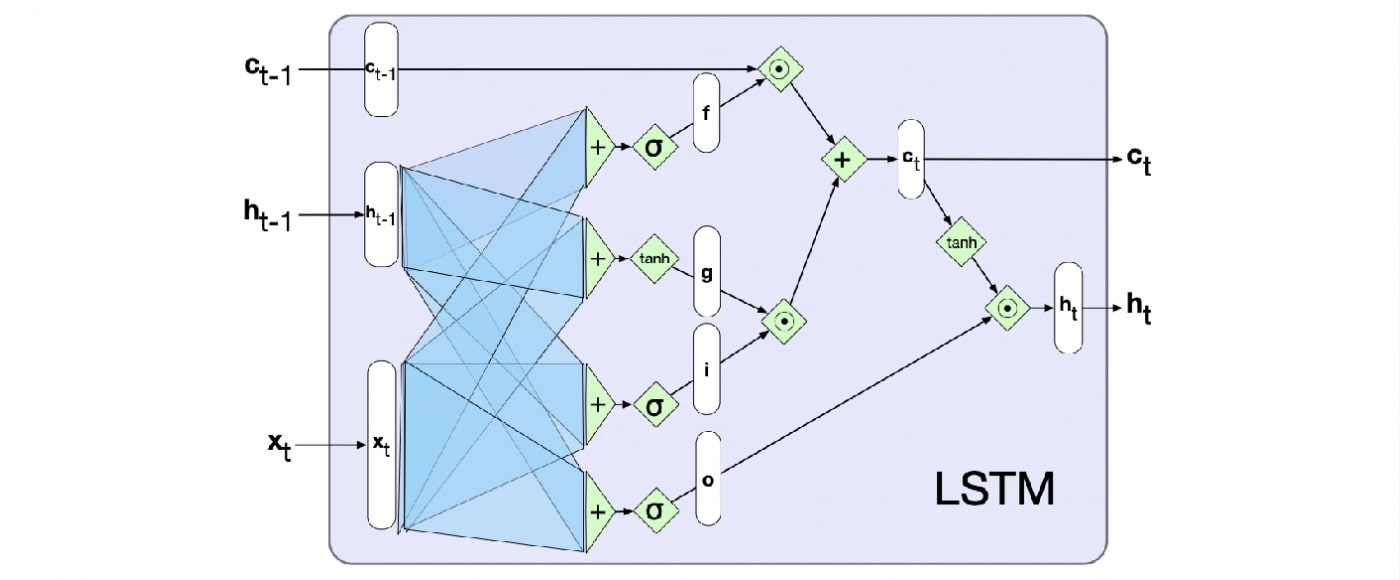
Gate

• Learn some mask (i.e., vector) via backpropagation
• Apply the mask(i.e., elementwise multiplication) to some hidden state

Computation

• Compute “current” state, “add” gate, “forget” gate, and “output” gate from previous hidden state and current input.
  • g = current state
  • f = forget gate
  • i = add gate
  • o = output gate (controls what to output and retains the relavant info right now.)
  • k = intermediate output (context after “forgetting”)
  • j = intermediate output (info to be added to the context)
  • c = updated context
  • h = updated hidden state
• Combine those things using Hadamard product.
• Update context and hidden state for next iteration.

$$g=\tanh \left(U_{g} h_{t-1}+W_{g} x_{t}\right) $$ $$f=\operatorname{sigmoid}\left(U_{f} h_{t-1}+W_{f} x_{t}\right) $$ $$i_{t}=\operatorname{sigmoid}\left(U_{i} h_{t-1}+W_{i} x_{t}\right) $$ $$o_{t}=\operatorname{sigmoid}\left(U_{o} h_{t-1}+W_{o} x_{t}\right) $$ $$k_{t}=f_{t} \odot c_{t-1} $$ $$j_{t}=i_{t} \odot g_{t} $$ $$c_{t}=j_{t}+k_{t} $$ $$h_{t}=o_{t} \odot \tanh \left(c_{t}\right) $$

Transformer

Architecture

Representation of the word depends on (slightly less contextualized) representation of other words.

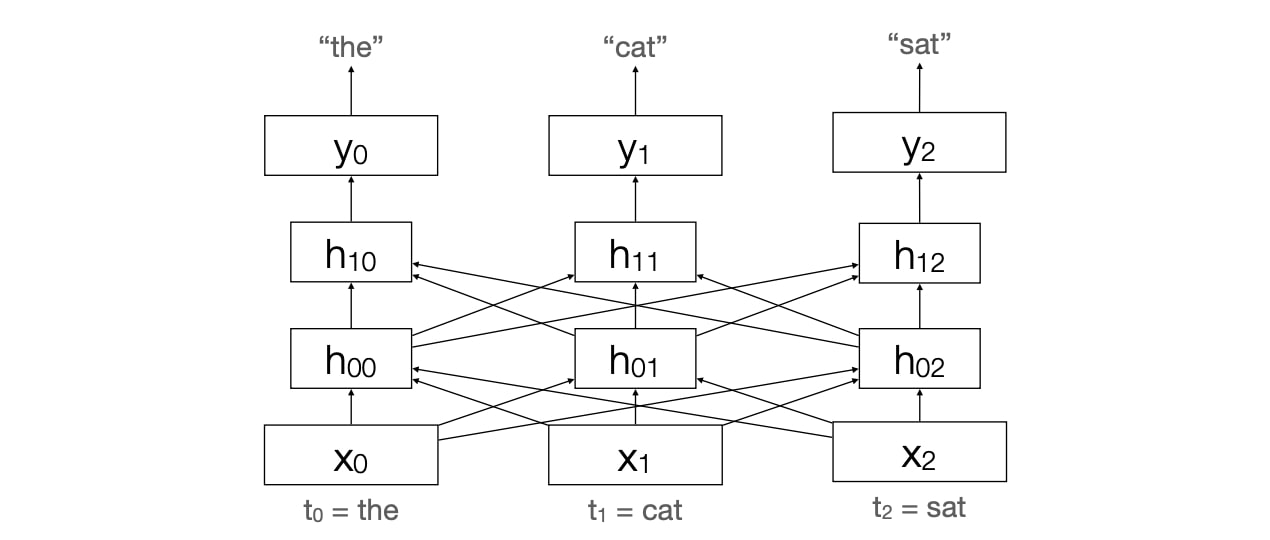
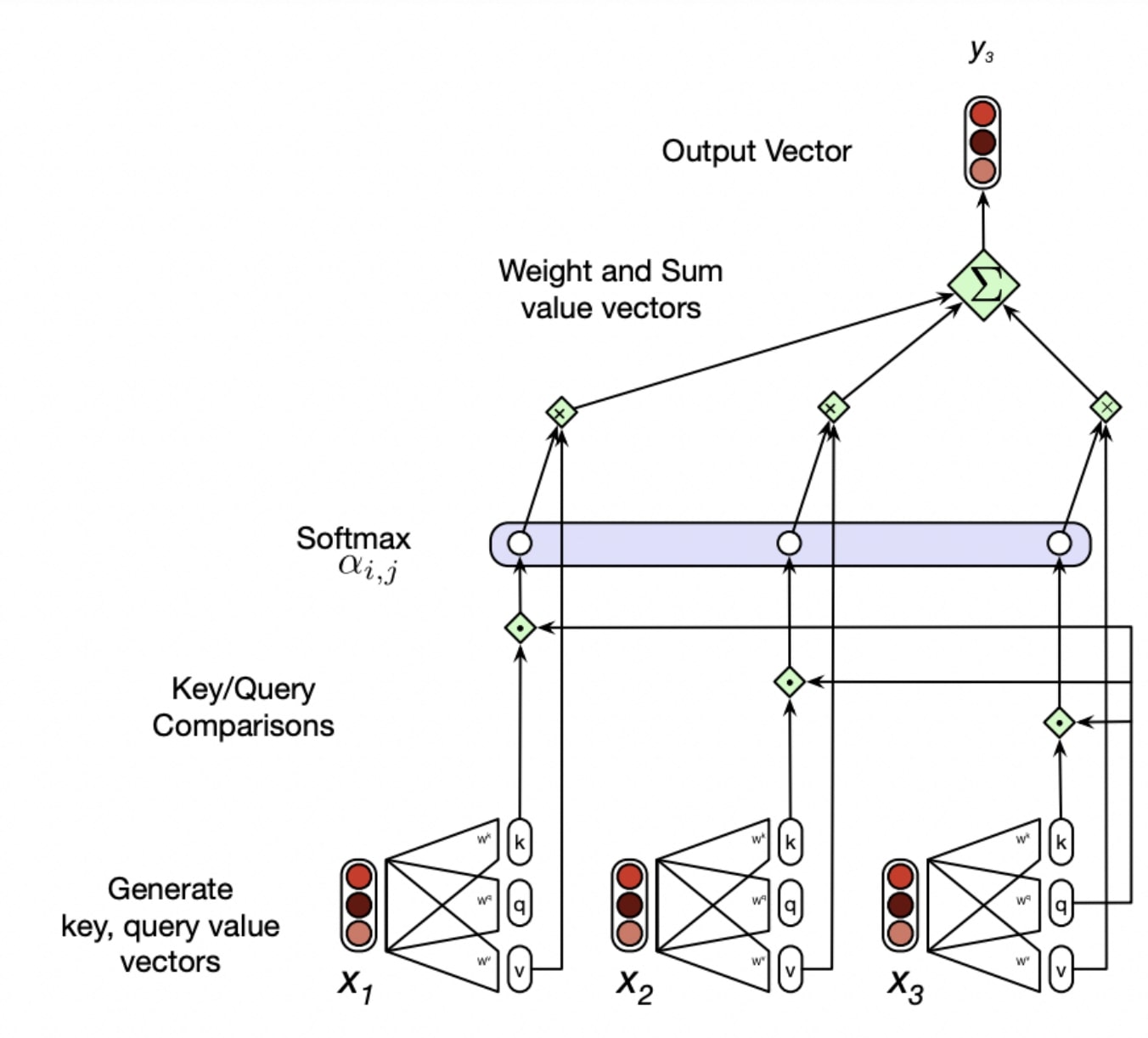
Self Attention

The idea is to learn a distribution/weighted combination of hidden states that inform this hidden state.

Each word has three roles at each timestep and we learn three weight matrices $(Q,K,V)$ to cast each word into each role. The dot product of key and Query produces a weight and the next layer receives the weighted combination of values.

• Query: The word as the current focus
• Key: The word as a context word
• Value: The word as part of the output

Multi-threaded self-attention is repeating the attention process multiple times. Each KQV set can focus on a slightly different aspect of the representation.

Blocks

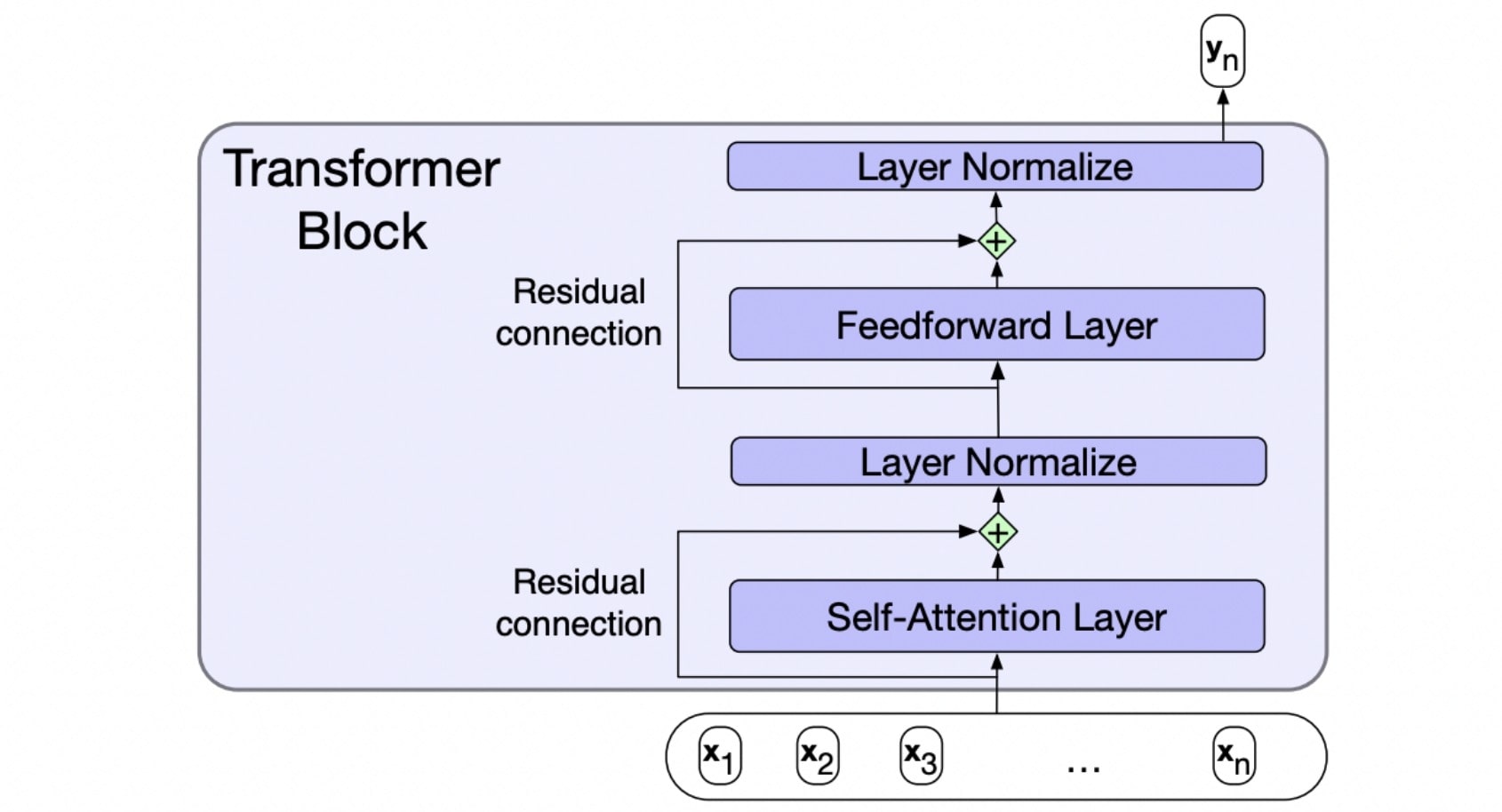
Residual Connection

It adds input to output to help with training/vanishing gradients.

Layer Normalize

It has the same idea of Z-score normalization.

Feedforward Layer

It is a simple perceptron-style layer to combine everything togethrt.

Positional Encoding

Transformers aren’t actually aware of the order in which words occur, becasue they are a bag of words essentially.

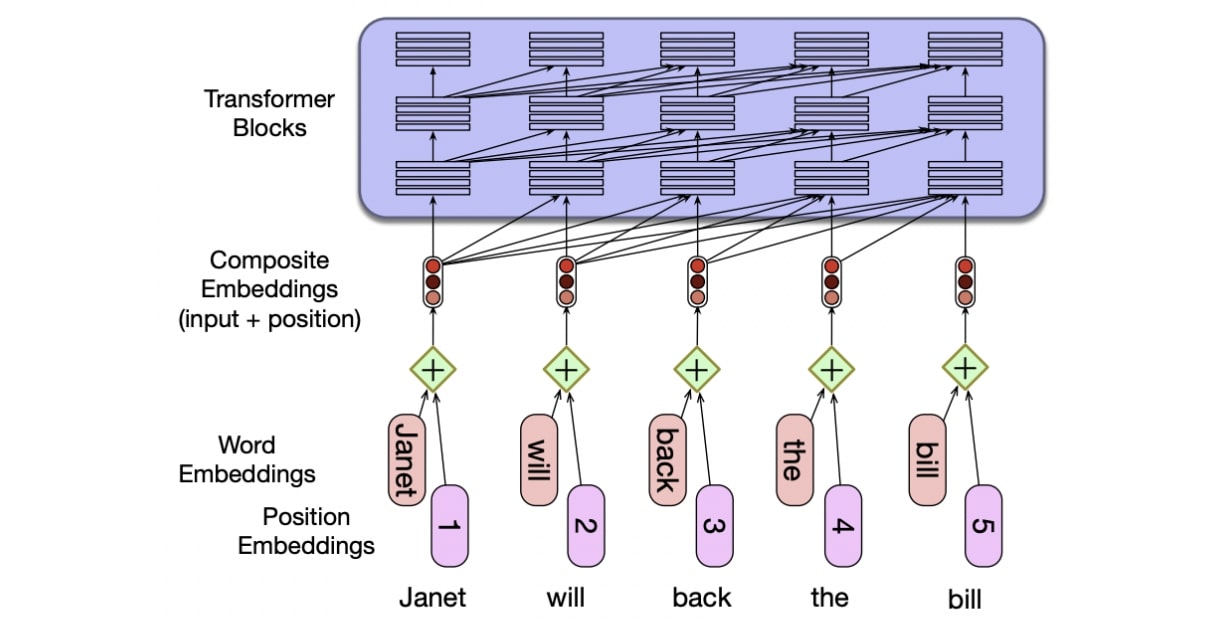
Positional encodings add an embedding representation of the absolute position to the input word embedding. However,

• Not the same as relative/order information in language
• Less supervision for later positions
• Hard to deal with recursive human language

why is it a big deal?

• Attention
  • has minimal inductive bias
  • can learn arbitrary graph structure
• Multiheadedness
  • Each “head” focuses on a different subspace of the input
• Scalability
  • At layer N, no dependency between timesteps, so it can be trained in parallel
  • Faster training = bigger models + more data
  • Allows for massive pretraining