Authored by Tony Feng

Created on Nov 10th, 2022

Last Modified on Nov 10th, 2022

Intro

This sereis of posts contains a summary of materials and readings from the course CSCI 1460 Computational Linguistics that I’ve taken @ Brown University. The class aims to explore techniques regarding recent advances in NLP with deep learning. I posted these “Notes” (what I’ve learnt) for study and review only.

Part of Speech Tags

Sequence Labeling Tasks

In linguistics, tags are descriptive to help us understand the constraints on grammar and meaning. In NLP, tags are used as features, which provide information that is important for understanding sentence, anticipating next words, etc.

• POS Tagging: NOUN, VERB, ADJ, …
• Named Entity Recognition (NER): PERSON, LOCATION, ORG, …
• Goal: Given words, predict tags

Ambiguity

• One word may have more than one possible tag.
• It is usually easy to tell from context.
• Most frequent class baseline: when ambiguous, guess the most likely tag given the training data.

Markov Models

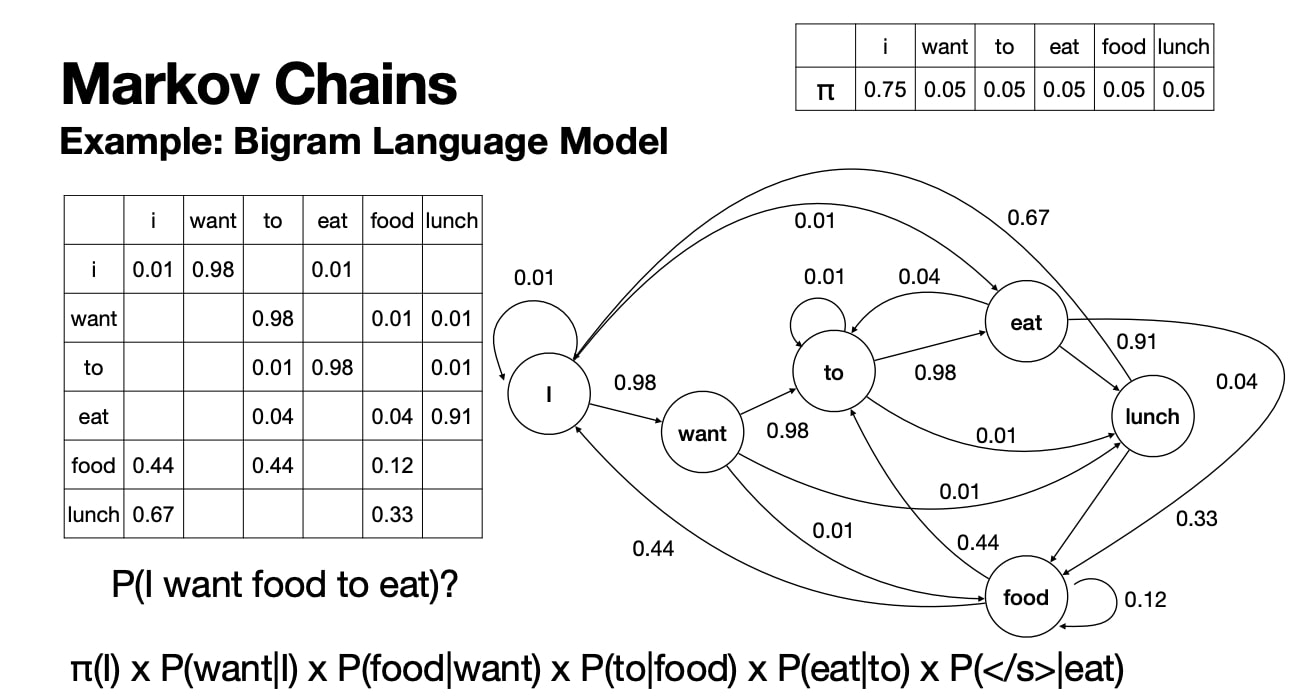
Markov Chains

• Markov Assumption: state $t+1$ depends only on state $t$.
  • $P(t+1 \mid t_0, …,t)=P(t+1 \mid t)$
  • Similar to a bigram language model
• Markov Chain is a simple model based on the assumption.
• Formal Def
  • $Q=\{ q_{1}, q_{2}, …, q_{N}\}$: a set of states
  • $A=\{a_{i,j}\}$: a transition probability matrix
  • $\pi=\{\pi_{1}, \pi_{2}, \ldots \pi_{N}\}$: an initial probability distribution over states

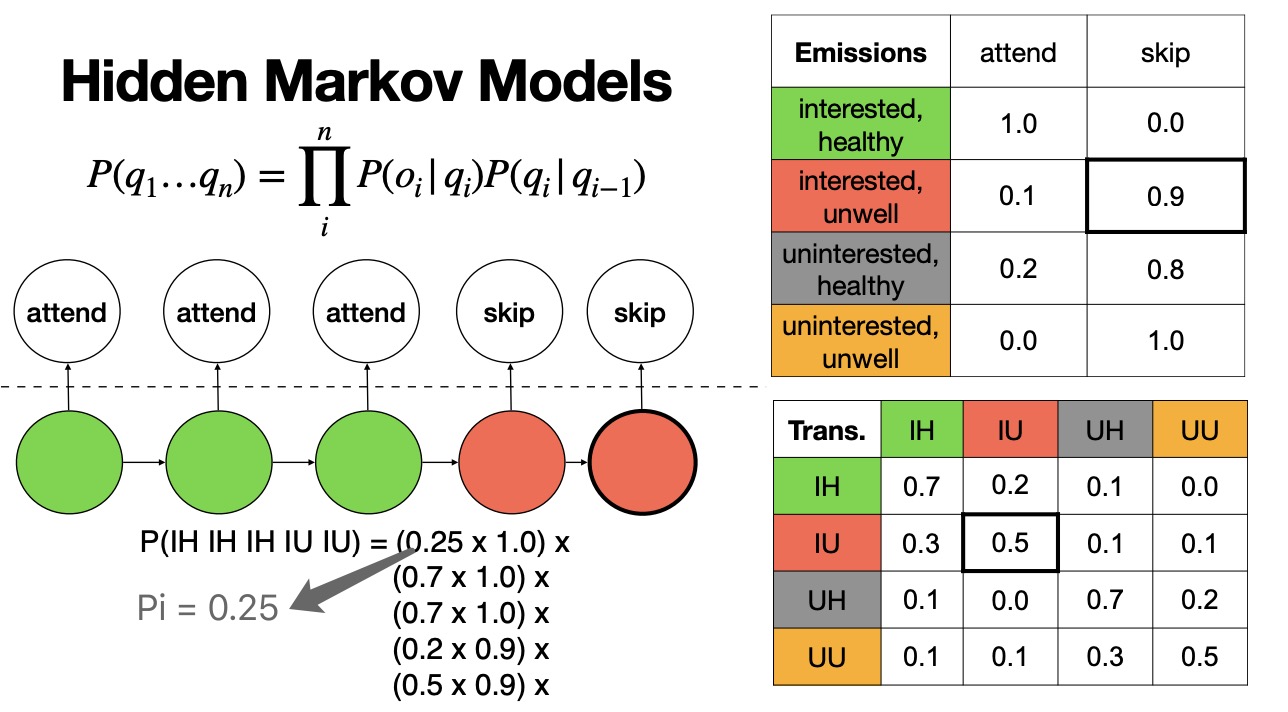
Hidden Markov Models

• Hidden or Latent factors are not directly observed, but they can nonetheless influence events which are observed.
  • Observed = func(Latent)
• Two Assumptions in HMM
  • Markov: $P(q_{t+1} \mid q_{0} \ldots q_{t})=P(q_{t+1} \mid q_{t})$
  • Output Independence: $P(o_t \mid o_0 \ldots o_n, q_0…q_n)=P(o_t \mid q_t)$
• Formal Def
  • $Q=\{ q_{1}, q_{2}, …, q_{N}\}$: a set of states
  • $A=\{a_{i,j}\}$: a transition probability matrix
  • $\pi=\{\pi_{1}, \pi_{2}, \ldots \pi_{N}\}$: an initial
  • $O=\{o_{1}, o_{2}, …, o_{N}\}$: a set of observations
  • $B=\{b_{i,j}\}$: an emission probability matrix specifying probability of observation $o_j$ given state $q_i$.
  • $\hat{q} = \text{argmax}_{Q} P(Q \mid O)$

To find $\hat{q}$, we can convert the problem into $\hat{q} = \text{argmax}_{Q} P(O \mid Q) P(Q)$.

• Markov (Emission): $P(Q)\approx \prod_{i=1}^{n} P\left(q_{i} \mid q_{i-1}\right)$
• Output Independence (Transition): $P(O \mid Q)\approx \prod_{i=1}^{n} P\left(o_{i} \mid q_{i}\right)$

In language, POS is latent, it is not observed. So, we can use an HMM to find the most likely POS sequence for a sentence. We can estimated by manually tagging a corpus and then counting up occurrences.

Viterbi Decoding

• Viterbi Algorithm is used to maximize $P(o_i \mid q_i)P(q_i|q_{i-1})$.
• It is a dynamic programming algorithm for decoding (finding the most likely output sequece).
• Formal Def

$$M[j][t]={max}_{i}^{n} M[i][t-1]*A[i][j]*B[j][t]$$

- Maintain $M$: a matrix with # of states x # of outputs
- $M[i][j]$ represents the probability of being in state $i$ after seeing outputs $0…j$
- $j$ is the current state (tag)
- $i$ is the previous state (tag)
- $t$ is current observation (word)
- $A$ is transition
- $B$ is emission

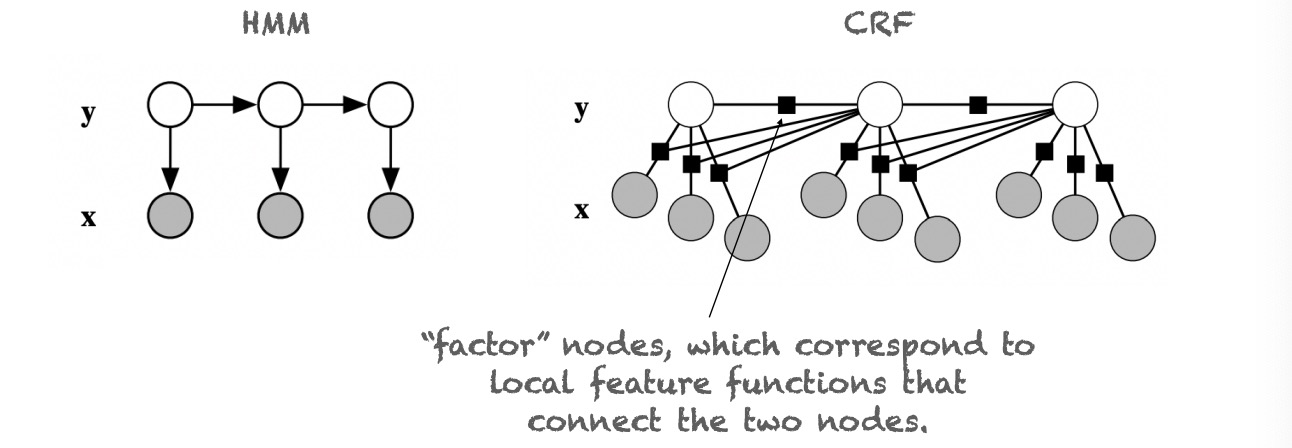
Conditional Random Fields

• HMMs struggle with unknown words.
• It is hard to incorporate all these features into an HMM.
• Using discriminative (log-linear) models to model the condition distribution directly.