[Comp Linguistics] Statistical Machine Translation

Authored by Tony Feng

Created on Nov 1st, 2022

Last Modified on Nov 10th, 2022

Intro

This sereis of posts contains a summary of materials and readings from the course CSCI 1460 Computational Linguistics that I’ve taken @ Brown University. The class aims to explore techniques regarding recent advances in NLP with deep learning. I posted these “Notes” (what I’ve learnt) for study and review only.

Language Diversity and Challenges

Perfect translation is not possible
Morphology
- Isolating vs. polysynthetic
- Agglutinative vs. fusional languages
Syntax
Agument structure and marking
- Possession
- Motion, manner
Referential Density
Lexicon: Every language has both polysemy and redundancy

Noisy Channel Models for SMT

Noisy Channel Model

Consider a message sent across a noisy channel. To determine the message, you need to correct for the noise that was added.

$$ P(\operatorname{tgt} \mid \operatorname{src}) \propto P(\operatorname{src} \mid \operatorname{tgt}) P(\operatorname{tgt}) $$

,where $P(\operatorname{src} \mid \operatorname{tgt})$ is translation model and $P(\operatorname{tgt})$ is language model.

Translation Model

Word Alignment

Bitext / Bilingual Parallel Corpora is a corpus that contains translated pairs of texts.

Document-level or Sentence level
Word-level alignment is rare

IBM Model 1

IBM Model 1 is the 1st (simplest) automatic unsupervised alignment model from IBM.

Choose length $L$ for source sentence
Choose an alignment $A = a_1 … a_L$
Generate target position $t_i$ by translating whatever source phrase is aligned to position $i$ in the target
Find the alignment that makes each observed source word most likely given its aligned target word

Dilemma:

We want alignments so that we can figure out the probabilities of phrase translations
To estimate those alignments, we need phrase translation probabilities

EM Algorithm

Expectation Maximization Algorithm is an optimization algorithm for generative models. It works for

If $P(a)$, then $P(b)$ can be computed.
If $P(b)$, the $P(a)$ can be computed.

Basic idea:

Randomly guess what $P(a)$ is
Use it to compute $P(b)$
Then, with your newly computed $P(b)$, recompute $P(a)$
Iterate until convergence

Language Model

Greedy Search

Finding best translation (e.g., arg-maxing $P(s|t)P(t)$) is just a search problem!

Greedy Search (Just for intuition)
Beam Search (more common)

Beam Search

Finding the most optimal sequence is computationally hard, since the search space increases exponentially. Beam Search considers the top K at each time step.

At first time step, choose k most likely words to be the initial “hypotheses”.
Theb, the top $K$ best hypotheses are carried forward, (i.e., softmax over the whole vocab given each hypothesis, so $K*V$ computations)
When </s> is generated, the generation is output.
Continue until beam is empty

Problems:

Heuristic and still not guaranteed to find best solution.
Hard to deal with long range dependencies.
Slow and memory intensive.

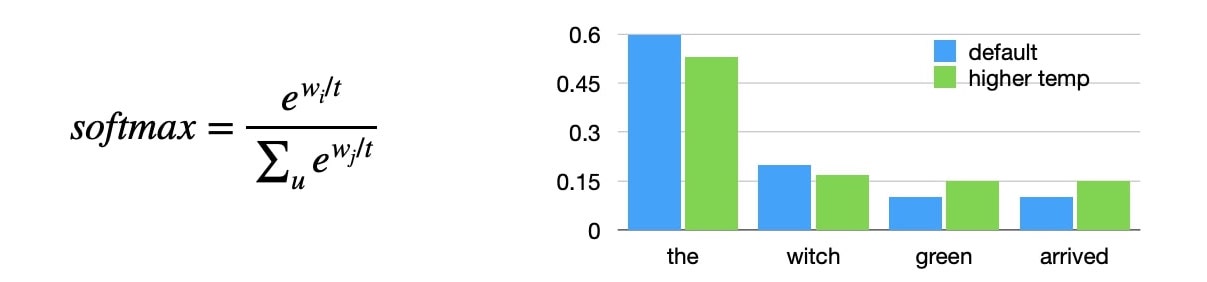
In practice, we often apply sampling $K$ continuations, rather than choosing the top $K$, which is controled by a temperature parameter.

Higher temperature = more oversampling of lower probability continuations
A low temperature (below 1) makes the model more confident.
A high temperature (above 1) makes the model less confident.
Intuition: “flatter” distribution

softmax with temperature

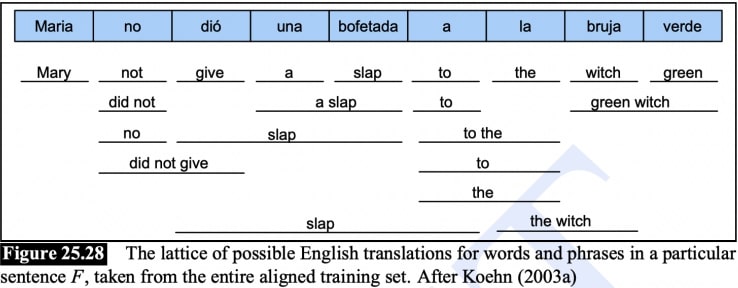
Full Phrase-Based MT System

$$ \operatorname{cost}(E, F)=\prod_{i \in S} \phi\left(\overline{f_{i}}, \overline{e_{i}}\right) d\left(a_{i}-b_{i-1}\right) P(E) $$

The cost is the product of all positions in the partial sentence, including translation probability, distortion probability, and language model probability.

Reference: