[Comp Linguistics] Text Classifier: ML Models

Authored by Tony Feng

Created on Sept 16th, 2022

Last Modified on Sept 16th, 2022

Intro

This sereis of posts contains a summary of materials and readings from the course CSCI 1460 Computational Linguistics that I’ve taken @ Brown University. The class aims to explore techniques regarding recent advances in NLP with deep learning. I posted these “Notes” (what I’ve learnt) for study and review only.

Supervised Classification

Supervised vs. Unsupervised

Supervised: I have lots of sentences. Given words 1…k in a sentence, can I predict word k+1? Unsupervised: I have a ton of news articles. Can I cluster them into meaningful groups?

Classification vs. Regression

Classification: Is the sentiment positive or negative?
Regression: How many likes will this tweet get?

Feature Matrices and BOW Models

Building Feature Matrices

ML models require input to be represented as numeric features, which could be encoded in a feature matrix.

Bag of Words Mode

It’s a model that uses the words as features. 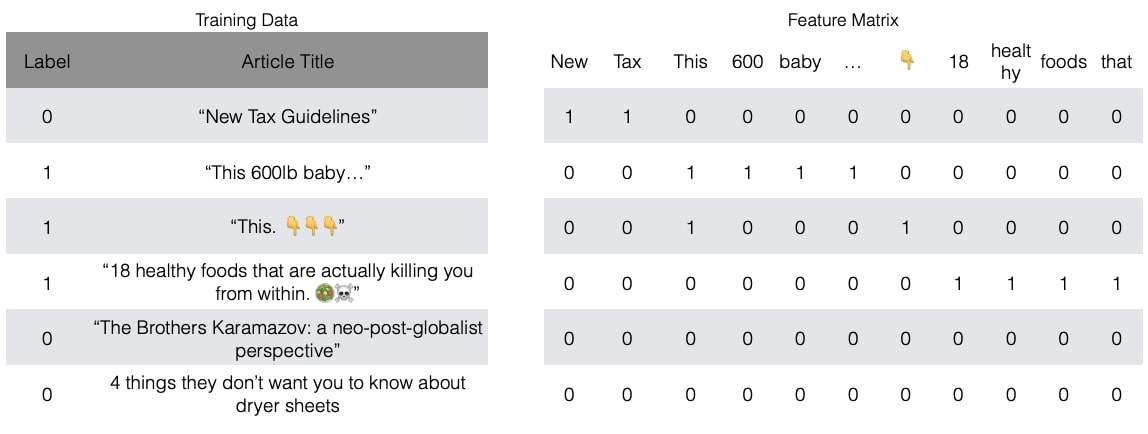BoW

No information about order or syntax
Binary representation
High Dimension

Naive Bayes Text Classifier

It is based on Bayes Rule to estimate/maximize $P(Y|X)$. $$ P(Y \mid X)=\frac{P(X,Y)}{P(X)} = \frac{P(X \mid Y) P(Y)}{P(X)} $$

We can apply chain rule to compute $ P(Y \mid X) = P(Y \mid x_{1}, x_{2}, \ldots, x_{k}) $ if there are multiple features maching the class: $$ P(Y \mid X) = P(x_{1} \mid x_{2}, \ldots, x_{k}, Y) P(x_{2} \mid x_{3}, \ldots, x_{k}, Y) \ldots P(x_{k} \mid Y) P(Y) $$

According to Naive Assumption, we assume features are independent. $$ P(Y \mid X) = P(x_{1} \mid Y) P(x_{2} \mid Y) \ldots P(x_{k} \mid Y) P(Y) $$

Now, we can easily compute the result. Note that $ P(Y) $ could be obtained through domain knwoledge or could be estimated from data.

Logistic Regression Text Classifier

LR vs. NB

Logistic Regression	Naive Bayes
Conditional Distribution $P(Y \mid X)$	Joint Distribution $P(X,Y)$
Discriminative Model	Generative Model
Maybe better in general	Better with smaller data

Logistic Regression Overview

Logistic Regression is based on Linear Regression, and is for classification.

$$ y=\frac{1}{1+e^{-(\vec{w} \cdot \vec{x})}} $$

$$ L = -Y \log \hat{Y}+(1-Y) \log (1-\hat{Y}) $$

Experimental Design in ML

Overfitting

Models overfit when then model idiosyncrasies of the training data that don’t necessarily generalize.

Train-Test Splits

Train: Used to train the model, i.e., set the parameters
Dev: Used during development, to inspect and choose “hyperparameters”
Test: In good experimental design, only allowed to evaluate on test one time to avoid “cheating”

i.i.d.: Train and Test data are drawn from the same distribution. In reality, test isn’t always i.i.d.

Common Baselines

Guess at random
State-of-the-art (SOTA)
Task-specific Heuristics
“Most frequent class”
“Skylines”, e.g. human performance, result under ideal conditions