Authored by Tony Feng
Created on Oct 6th, 2022
Last Modified on Oct 6th, 2022
Intro
This sereis of posts contains a summary of materials and readings from the course CSCI 1460 Computational Linguistics that I’ve taken @ Brown University. The class aims to explore techniques regarding recent advances in NLP with deep learning. I posted these “Notes” (what I’ve learnt) for study and review only.
Topic Model
What is Topic Model?
It’s a method for automatically organizing a collection of a text and is used for unlabled document collections.
- Topics are defined as combinations of words.
- Documents are defined as combinations of topics.
“Since you read an article about basketball, you might also like other articles about basketball.”
“In the past year, people have been talking more about the economy than about schools.”
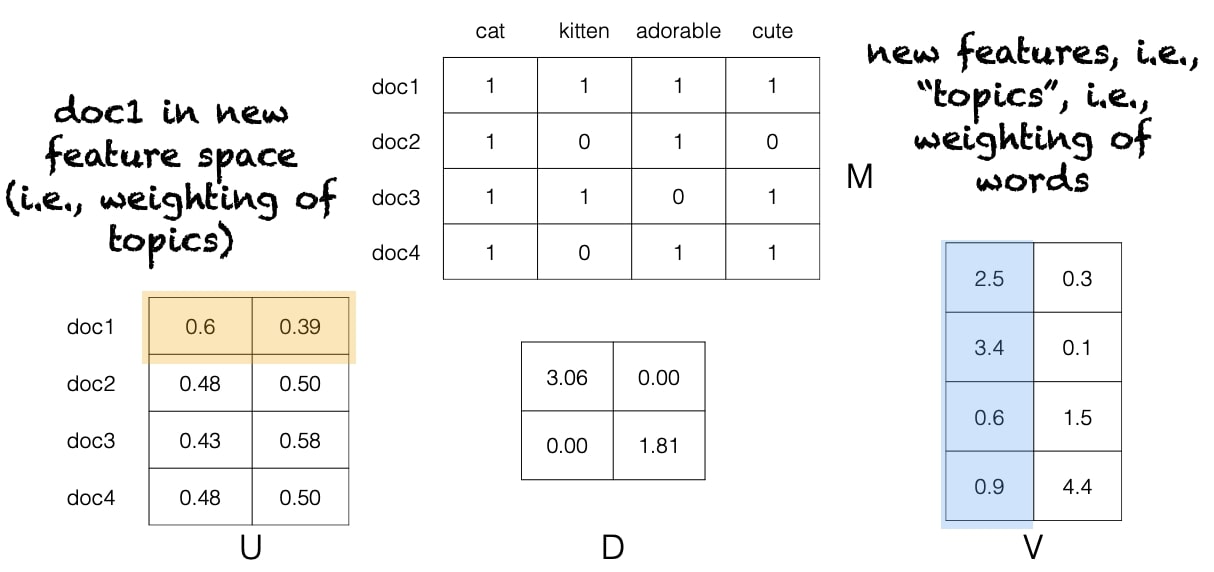
Latent Semantic Analysis (LSA)
It uses dimensionality reduction/linear algebra to generate a topic model.


Latent Dirichelet Allocation (LDA)
It uses probability models/graphical models in contrast to LSA which has no notion of probability.
Generative Stories
It’s the first step to build models that makes assumptions about the structure of the data or problem, which tells a story about how the observed data came to be.
Repeat:
- Sampling a topic
- Sampling a word from that topic
However, we need to further associate them with syntax, word order, semantics, discourse, etc.
$$ P\left(w_{i}\right)=\sum_{j=1}^{T} P\left(w_{i} \mid z_{i}=j\right) P\left(z_{i}=j\right) $$
, where $ P\left(w_{i}\right)$ is the probability of the data (a given word), $P\left(w_{i} \mid z_{i}=j\right)$ is the probability of that word for a given topic, $P\left(z_{i}=j\right)$ is overall probability of that topic.
Given the observed word, find the $P(z)$ and $P(w|z)$ that make the observed word most likely.

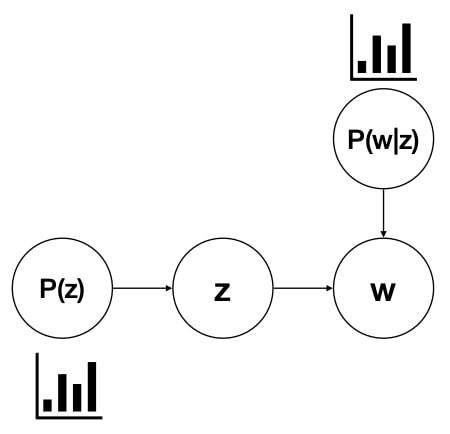

Graphical Model Notation

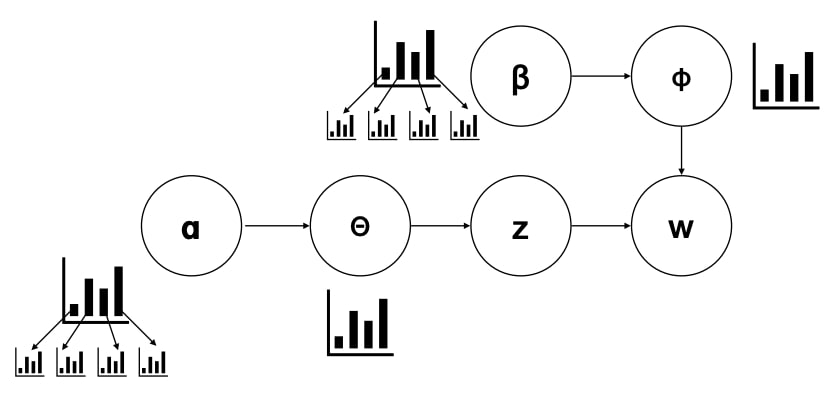

$z$ and $w$ depend on multinomial distribution of $P(z)$ and $P(w|z)$ respectively. Then, we assume those distributions come from a Dirichlet distributions $ \alpha $ and $\beta$.
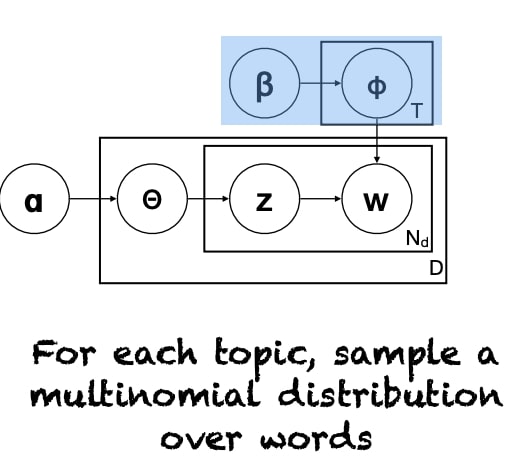
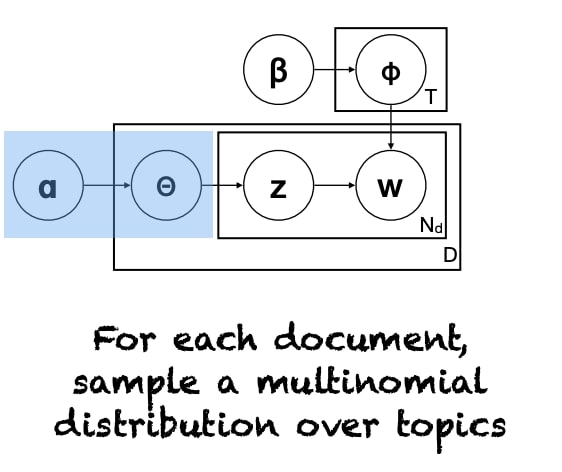
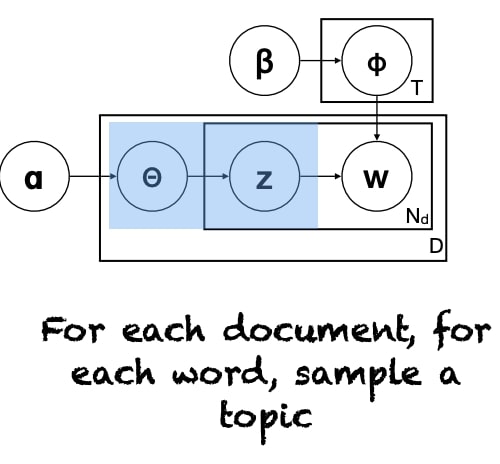
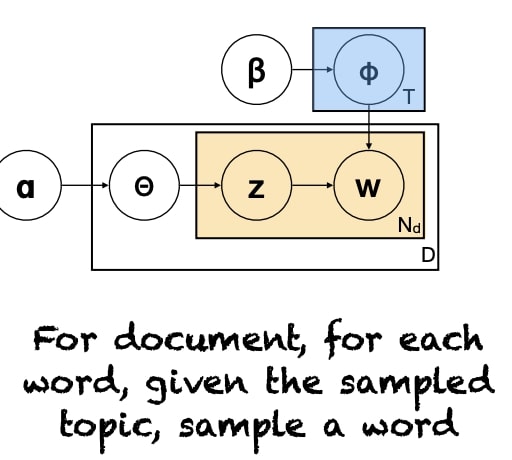
Training & Evaluation
We resort to approximate methods for posterior estimation.
- Sampling Methods (MCMC, Gibbs Sampling)
- Variational Inference