Authored by Tony Feng

Created on Feb 2nd, 2022

Last Modified on Feb 9nd, 2022

Intro

This sereis of posts contains a summary of materials and readings from the course CSCI 1430 Computer Vision that I’ve taken @ Brown University. This course covers the topics of fundamentals of image formation, camera imaging geometry, feature detection and matching, stereo, motion estimation and tracking, image classification, scene understanding, and deep learning with neural networks. I posted these “Notes” (what I’ve learnt) for study and review only.

Fourier Series

A General Idea

Any univariate function can be rewritten as a weighted sum of sines and cosines of different frequencies.

$$F_{Target} = F_{1}+F_{2}+F_{3} \ldots$$

Here is the sine-cosine form

$$F = \sum_{n=1}^{\infty}\left(a_{n} \cos (n t)+b_{n} \sin (n t)\right)$$

Spatial and Frequency Domain

Amplitude & Phase

We can convert ine-cosine representation to amplitude-phase form.

$$F = \sum_{n=1}^{\infty}\left(a_{n} \sin \left(n x+\emptyset_{n}\right)\right)$$

Amplitude encodes how much signal there is at a particular frequency, while Phase encodes spatial information. In other words, Amplitude tells you “how much” and Phase tells you “where”.

Fourier transform

Computing the Fourier Transform

Continuous

$$H(\omega)=\int_{-\infty}^{\infty} h(x) e^{-j \omega x} d x$$

Discrete

$$H(k)=\frac{1}{N} \sum_{x=0}^{N-1} h(x) e^{-j \frac{2 \pi k x}{N}} \quad ,k=-\frac{k}{2} … \frac{k}{2}$$

Properties of Fourier Transforms

• Linearity $\mathrm{F}[a x(t)+b y(t)]=a \mathrm{~F}[x(t)]+b \mathrm{~F}[y(t)]$
• Fourier transform of a real signal is symmetric about the origin.
• The energy of the signal is the same as the energy of its Fourier transform.

Gaussian Filter Duality

Fourier transform of one Gaussian is another Gaussian (with inverse variance).

Why is this useful?

• Smooth degradation in frequency components
• No sharp cut-off
• No negative values
• Never zero (infinite extent)

2D Discrete Fourier Transform

$$F[u, v]=\frac{1}{M N} \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} I[m, n] \cdot e^{-i 2 \pi\left(\frac{u m}{M}+\frac{v n}{N}\right)}$$

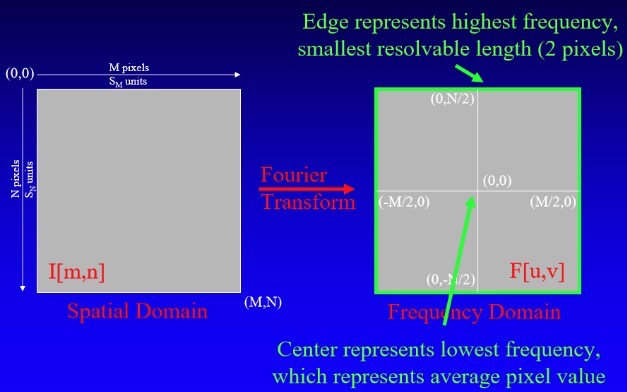
Nyquist frequency is half the sampling rate of the signal. Sampling rate is size of image $M*N$, so Fourier transform images are ($\pm \frac{N}{2} $, $\pm \frac{N}{2} $).

Image is rotationally symmetric about center because of negative frequencies.

If we have infinite frequencies, why does the image end?

• Frequencies higher than Nyquist frequency end up falling on an existing sample.
• Nyquist frequency is half the sampling frequency.

Fourier Decomposition Image

Intuitively, we can obtain the image by correlating the signal with a set of waves of increasing frequency.

• In 2D, $O(N^2)$ operation
• For Fast Fourier Transform (FFT), $O(NlogN)$ (effective for larger image)

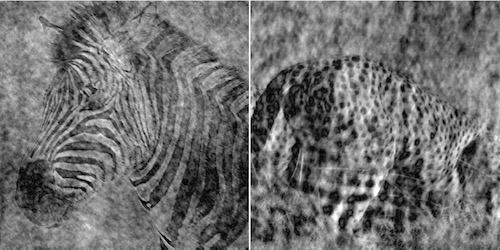
The first row is set of the Fourier amplitude images and the second row is set of spatial domain imahe.

The frequency amplitude of natural images are quite similar. Most information in the image is carried in the phase, not the amplitude. In Fourier space, Phase is more of the information that we see in the visual world.

The Convolution Theorem

The Fourier transform of the convolution of two functions is the product of their Fourier transforms.

$$F[g \otimes h] = F[g]F[h]$$

Convolution in spatial domain is equivalent to multiplication in frequency domain.

$$g \otimes h=\mathrm{F}^{-1}[\mathrm{~F}[g] \mathrm{F}[h]]$$

If convolution is just multiplication in the Fourier domain, isn’t deconvolution just using division?

• Sometimes, it clearly is invertible (e.g. a convolution with an identity filter)
• In one case, it clearly isn’t invertible (e.g. convolution with an all zero filter)
  • A Gaussian is only zero at infinity, so it is invertible.

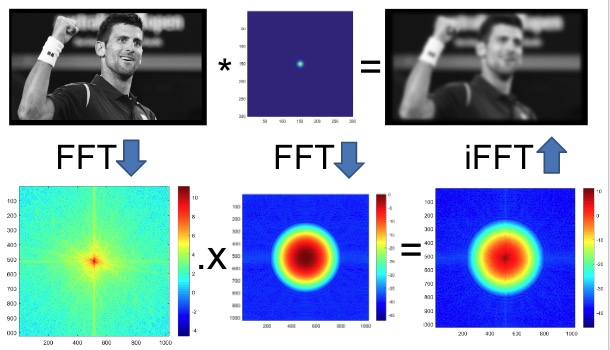
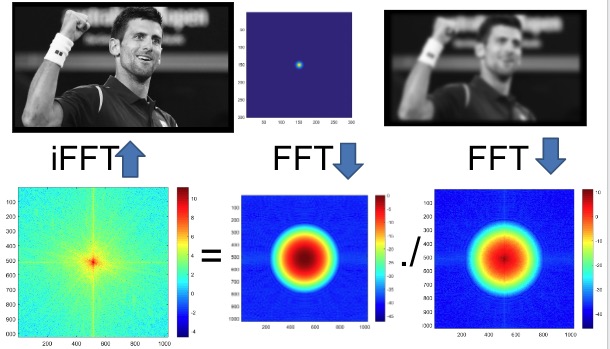
Filtering in Frequency Domain

• Convert image and filter to Fourier domain
• Element-wise multiply their decompositions
• Convert result to spatial domain with inverse Fourier transform