Authored by Tony Feng

Created on Feb 23th, 2022

Last Modified on Feb 23th, 2022

Intro

This sereis of posts contains a summary of materials and readings from the course CSCI 1430 Computer Vision that I’ve taken @ Brown University. This course covers the topics of fundamentals of image formation, camera imaging geometry, feature detection and matching, stereo, motion estimation and tracking, image classification, scene understanding, and deep learning with neural networks. I posted these “Notes” (what I’ve learnt) for study and review only.

Camera Matrix Model

Now, we have the camera matrix model

$$x_{\text{image}} = K\left [ R\mid t \right ] X_{\text{world}}$$

Camera Simulation
We know camera parameters and the world coordinates of an object, the goal is to get its position in an image.

Camera Calibration
We know the world coordinates and image coordinates of an object, the goal is to calculate the camera matrices.

3D Reconstruction
We know the camera parameters and image coordinates of an object, the goal is to get the world coordinates of an object. Sometimes, we don’t even know the camera parameters, and just use image coordinates of an object to estimate its world coordinates.

Solving Camera Parameters

When we calibrating the camera, we can combine $R$ and $t$ into a matrix $M$, whose dimension is $3 * 4$. How to get $M$, given $x_{\text{image}}$ and $X_{\text{world}}$?

Least Squares Regression

Given data $(x_1, y_1), (x_2, y_2), …, (x_n, y_n)$, how to find $a$ and $b$ to fit a linear equation $y = ax+b$?

$$ E=\sum_{i=1}^{n}\left(y_{i}-m x_{i}-b\right)^{2} = ||Y - XP || ^2$$

$$\Downarrow $$

$$ E= {Y}^{T} {Y}-2({XP})^{T} {Y}+({X} {P})^{T}({XP})$$

$$\Downarrow $$

$$ \frac{d E}{d P}=2 {X}^{T} {X} {P}-2 {X}^{T} {Y}=0$$

$$\Downarrow $$

$$ {P}=\left({X}^{T} {X}\right)^{-1} {X}^{T} {Y}$$

Matrix Computation

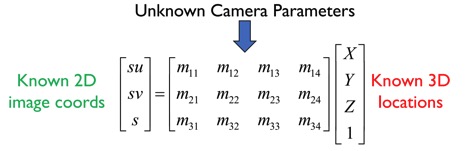
$$s u =m_{11} X+m_{12} Y+m_{13} Z+m_{14}$$

$$s v =m_{21} X+m_{22} Y+m_{23} Z+m_{24} $$

$$s =m_{31} X+m_{32} Y+m_{33} Z+m_{34} $$

$$\Downarrow $$

$$u =\frac{m_{11} X+m_{12} Y+m_{13} Z+m_{14}}{m_{31} X+m_{32} Y+m_{33} Z+m_{34}} $$

$$v =\frac{m_{21} X+m_{22} Y+m_{23} Z+m_{24}}{m_{31} X+m_{32} Y+m_{33} Z+m_{34}} $$

$$\Downarrow $$

$$ 0=m_{11} X+m_{12} Y+m_{13} Z+m_{14}-m_{31} u X-m_{32} u Y-m_{33} u Z-m_{34} u $$

$$ 0=m_{21} X+m_{22} Y+m_{23} Z+m_{24}-m_{31} v X-m_{32} v Y-m_{33} v Z-m_{34} v $$

$$\Downarrow $$

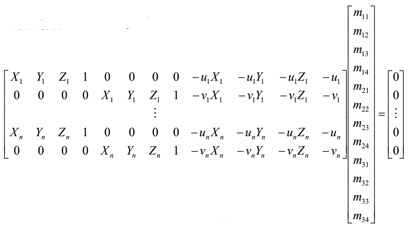
RQ Decomposition

We can decompose $M$ back to $K\left [ R\mid t \right ]$. Here is the link for more information.